Dependent t-test

การทดสอบ Dependent t-test หรือ paired-sample t-test คือการทดสอบค่าเฉลี่ยของกลุ่มสองกลุ่มที่ไม่เป็นอิสระจากกัน

“ไม่เป็นอิสระจากกัน คืออัลลลลไลลลล?”

ความไม่เป็นอิสระจากกันคือการที่ค่า x1 ในกลุ่ม 1 มีความสัมพันธ์กับ x1 ในกลุ่ม 2 เช่น

การเก็บข้อมูล Job Satisfaction ก่อนเข้า Training และ หลังการเข้า training

เราจะเรียกการทดสอบข้อมูลนี้ว่า repeated-measure t-test

หรือ

relationship Satisfaction เมื่อคะแนนเป็นของ สามี และ ภรรยา

ข้อตกลงเบื้องต้นของ Dependent t-test

ข้อตกลงเบื้องต้นของ Dependent t-test จะมีความคล้ายคลึงกับ Independent t-test

การวิเคราะห์ผลโดยนำค่าเฉลี่ยจากกลุ่มตัวอย่าง (X̄1a) ไปเปรียบเทียบกับค่าเฉลี่ยกลุ่มตัวอย่าง (X̄1b) ข้อมูลของกลุ่มตัวอย่างจำเป็นต้องผ่านข้อตกลงเบื้องต้น หรือ (assumption) ของการทดสอบสถิติดังกล่าว

ข้อตกลงเบื้องต้นของ Dependent t-test มีดังนี้

* ตัวแปรตาม (dependent variable) หรือตัวแปร criterion ควรอยู่ในรูปของตัวแปรต่อเนื่อง (see: levels of measurements) ไม่ว่าจะเป็นแบบ interval หรือ ratio

* ตัวแปรต้น (independent variable) ควรมีลักษณะเป็นกลุ่มจำนวน 2 กลุ่ม ที่มีความเป็นคู่กันอย่างตัวอย่างข้างต้น

* ข้อมูลไม่ควรมีค่าสุดโต่ง (outliers) เพราะการใช้ค่าเฉลี่ย (mean) ในการคำนวณมีความเสี่ยงจะเกิดอคติสูง (see concept ทำไมถึงใช้ค่าเฉลี่ย)

* ตัวแปรตาม (dependent variable) ควรอย่างน้อยมีโค้งเป็นปกติในแต่ละกลุ่ม แม้ว่าการทดสอบ t จะค่อนข้างแข็งแกร่ง (robust) ต่อการเบ้ของข้อมูลก็ตาม เราสามารถทดสอบได้ด้วย Shapiro-Wilk test of normality

เรามาสร้างข้อมูลกัน

สมมติว่า เราเป็นนักวิจัย ไปสอบถามความพึงพอใจในคู่ของตัวเอง โดยถามฝ่าย a และฝ่าย b (ที่ใช้ a,b เพราะต้อนรับสู่สังคม LGBTQ ค่า~) ได้คะแนนเฉลี่ยมาดังนี้

X̄a = 6.926 X̄b = 6.298; scale 1 - 10 Likert

set.seed(1990)
Agroup <- rnorm(100, mean = 7.12, sd = 1.2)
Bgroup <- rnorm(100, mean = 6.25, sd = 2.1)
summary(Agroup)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   3.968   6.032   6.736   6.789   7.435   9.998

summary(Bgroup)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -0.6295  4.9916  5.8712  6.1806  7.5041 10.7801

จากนั้นเราจะลองไปทดสอบข้อตกลงเบื้องต้นกันค่ะ

Outliers
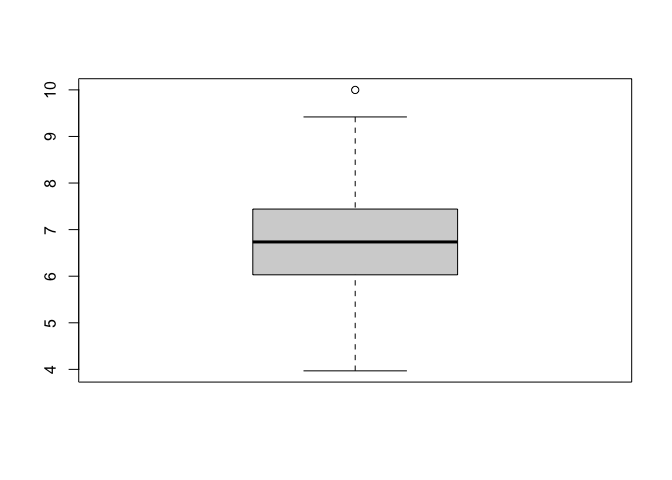
```
boxplot(Agroup)
```

boxplot(Bgroup)

จะเห็นว่ามีจุดสีขาวโผล่ขึ้นมาในกราฟ boxplot() ถ้าเราต้องการทดสอบ เราสามารถอ้างอิงจาก boxplot ด้วยการเขียน

boxplot(Agroup)$out

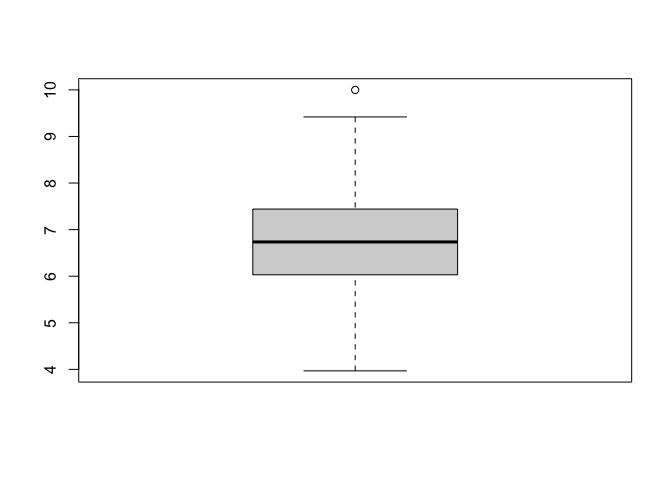
## [1] 9.99805

boxplot(Bgroup)$out

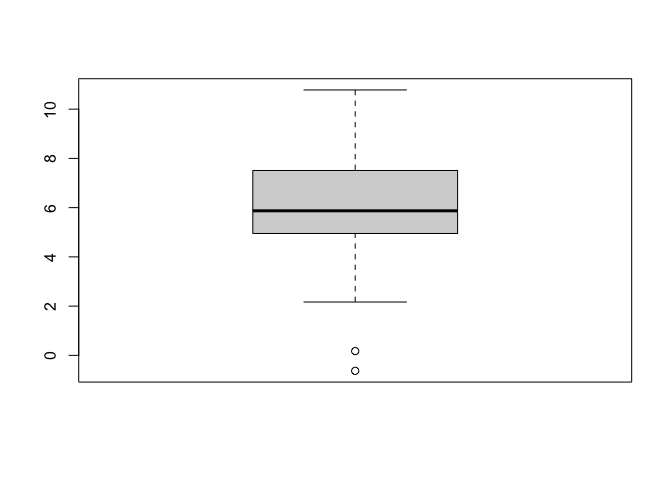
## [1] -0.6294601  0.1734488

ก่อนที่จะทำการจัดการข้อมูลนี้ เรามาดูว่า 2 ข้อมูลนี้ละเมิดข้อตกลงอื่นด้วยหรือไม่

ความเป็น normality

car::qqPlot(Agroup)

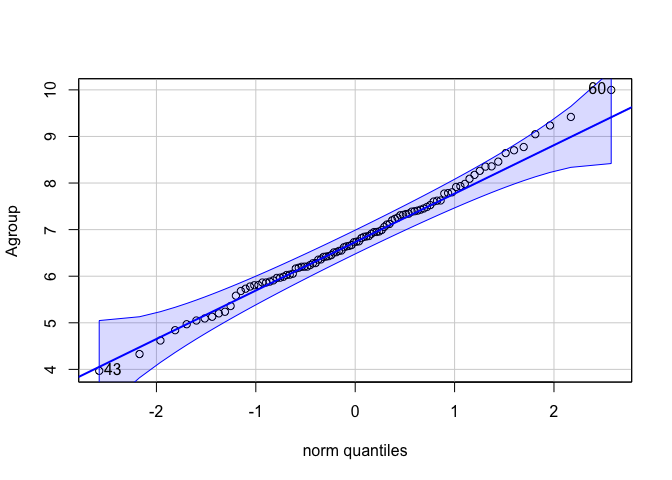
## [1] 60 43

car::qqPlot(Bgroup)

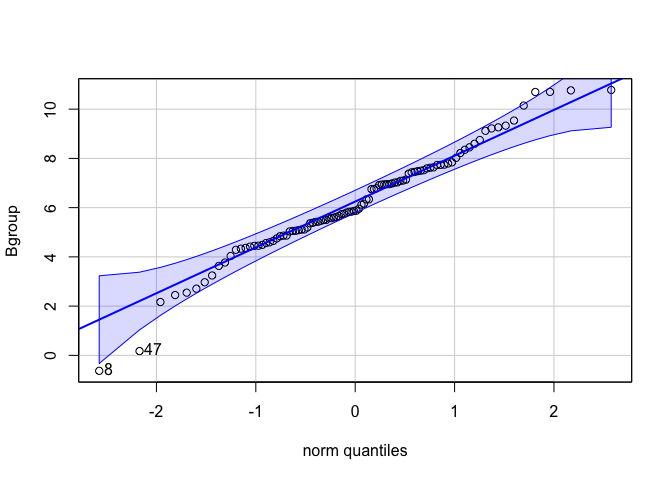
## [1]  8 47

ดูจาก qqPlot แล้วเหมือนจะไม่มีปัญหาเท่าไหร่นะ

เราจะมาเริ่มทดสอบ dependent t กันค่ะ

t.test(Agroup, Bgroup, paired = TRUE)

## 
##  Paired t-test
## 
## data:  Agroup and Bgroup
## t = 2.5734, df = 99, p-value = 0.01155
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.1393124 1.0775929
## sample estimates:
## mean of the differences 
##               0.6084527

ผล Output ของ R บอกเราว่าฝั่ง A กับฝั่ง B เค้ามีความพึงพอใจในความสัมพันธ์ (relationship satisfaction) แตกต่างกันที่ t(1,99) = 2.5734, p < 0.05 มีความแตกต่างของค่าเฉลี่ยอยู่ที่ 0.608

ตอนนี้ก็ไม่รู้ว่าฝั่ง A ได้ยินข้อมูลนี้แล้วจะรู้สึกยังไงบ้างเนอะ บางทีรักของเราก็ไม่เท่ากันเนอะ……… T^T

สร้างกราฟให้เป็นนิสัยกันดีกว่า

    # ทำให้เป็น data.frame ก่อน
    group <- data.frame(Agroup, Bgroup)
    library(ggplot2)
    ggplot(group) +
      geom_density(aes(x = Agroup, fill = "Agroup")) +
      geom_density(aes(x = Bgroup, fill = "Bgroup"), alpha = 0.5) +
      xlab("Difference Between A and B group") +
      theme_classic()

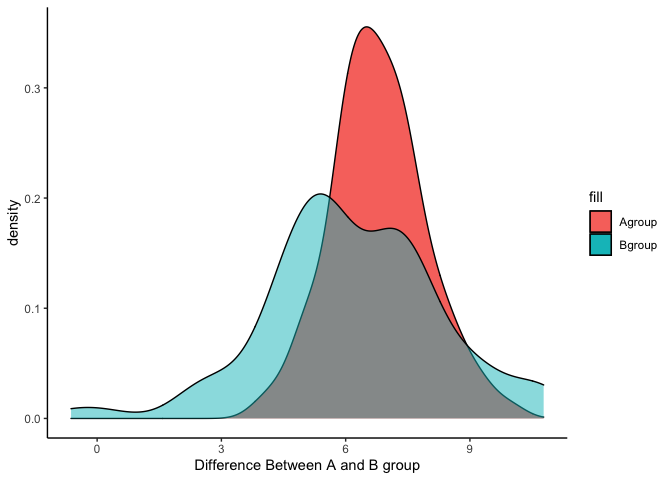
จะเห็นได้ว่าพื้นที่สีเทาคือจุดกราฟซ้อนกันบนช่วงค่าเฉลี่ยที่คร่อมกัน