Hirarchical Regression
Hirarchical Regression สมการถอดถอยแบบลำดับขั้น คือทดสอบสมการถอดถอยในอีกแบบหนึ่ง (ที่อาจจะมองว่าไม่ต่างจาก Multiple Regression เท่าไหร่นัก) โดยหลักแล้วคือการที่เราใส่ตัวแปรที่มองว่าเป็นตัวแปรที่เป็น 1. ตัวแปรควบคุม 2. ตัวแปรแทรกซ้อน 3.ตัวแปรที่ติดมากับบุคคลเช่น เพศ อายุ
เมื่อนำตัวแปรเหล่านี้เข้าไปใส่ในสมการ เราจะได้ผลที่เรียกว่า R^2 ออกมา (ดู Multiple Regression) จากนั้นเราถึงจะใส่ตัวแปรจริงลงไปในสมการเพื่อดูว่า R^2 เพิ่มขึ้นไหม หรืออีกมุมหนึ่งคือ ตัวแปรในการศึกษาของเราอธิบายโมเดลมากขึ้นหรือเปล่า
กรณีที่เกิดขึ้นก็จะมี 2 แบบ คือ
- 1. R^2 เพิ่มขึ้น แต่ผลทดสอบ Chi-square (model) ไม่ถึงนัยสำคัญ และ
- R^2 เพิ่มขึ้น และผลทดสอบ Chi-square (model) ถึงระดับนัยสำคัญ
เราลองมาเริ่มสร้างข้อมูลกัน
set.seed(1990)
gender <- c(rep("male", 50), rep("female", 50))
saving <- round(c(rnorm(50, 245, sd = 2.11), rnorm(50, 210, sd = 2.34)),2)
age <- round(c(rnorm(50, 31, sd = 2.1), rnorm(50, 28, sd = 1.76)))
household <- abs(round(c(rnorm(50, 3, sd = 1.4), rnorm(50, 2.7, sd = 1.2))))
data <- data.frame(gender, age, household, saving)
head(data)
## gender age household saving
## 1 male 33 3 243.01
## 2 male 29 3 245.51
## 3 male 32 2 243.39
## 4 male 32 4 245.24
## 5 male 30 2 243.94
## 6 male 31 3 248.72
summary(data)
## gender age household saving
## Length:100 Min. :24.00 Min. :0.00 Min. :205.1
## Class :character 1st Qu.:27.75 1st Qu.:2.00 1st Qu.:209.5
## Mode :character Median :29.00 Median :3.00 Median :227.5
## Mean :29.45 Mean :2.63 Mean :226.9
## 3rd Qu.:31.25 3rd Qu.:4.00 3rd Qu.:244.2
## Max. :36.00 Max. :7.00 Max. :248.7
psych::describeBy(saving, group = gender, data = data)
##
## Descriptive statistics by group
## group: female
## vars n mean sd median trimmed mad min max range skew kurtosis
## X1 1 50 209.42 2.31 209.44 209.32 2.41 205.12 215.61 10.49 0.38 -0.21
## se
## X1 0.33
## ------------------------------------------------------------
## group: male
## vars n mean sd median trimmed mad min max range skew kurtosis
## X1 1 50 244.36 1.9 244.24 244.37 1.71 239.46 248.72 9.26 -0.05 0.25
## se
## X1 0.27
จากข้อมูลที่สร้างขึ้นมาเอง จะมีตัวแปรดังต่อไปนี้คือ gender = เพศ ซึ่งจะเป็นตัวแปรต้นหลักของเรา age = อายุ household = จำนวนคนในครอบครัว และ saving = ค่าเฉลี่ยของเงินเก็บรายสัปดาห์
เมื่อเรียกคำสั่ง psych::describeBy(x, group = __, data) ออกมาแล้วจะพบว่าค่าเฉลี่ยของเงินเก็บจากเพศเป็นดังนี้
Descriptive statistics by group
group: female
vars n mean sd median trimmed mad min max range skew kurtosis se
X1 1 50 209.89 1.57 209.98 209.96 1.39 205.83 213.2 7.37 -0.36 -0.1 0.22
--------------------------------------------------------------------------------
group: male
vars n mean sd median trimmed mad min max range skew kurtosis se
X1 1 50 299.7 1.58 299.51 299.73 1.76 294.45 302.66 8.21 -0.47 0.76 0.22
ประเด็นที่น่าสนใจที่ไม่ได้กล่าวไว้ใน Multiple Regression คือ การมีตัวแปรกลุ่มในสมการถอดถอย
การมีตัวแปรกลุ่มใน multiple regression
เราสามารถนำตัวแปรแบบกลุ่มเข้าไปสมการถดถอยได้ โดยกลุ่มอ้างอิงจะเรียงตาม table() ที่เรามี
table(data$gender)
##
## female male
## 50 50
ผลแสดงว่ากลุ่มอ้างอิงที่ R สร้างให้คือกลุ่ม female = 0, และ male = 1
Note กลุ่มอ้างอิงนี้ เมื่อเพิ่มขึ้น เช่น มีเพศ หญิง ชาย และ LGBTQ เราจะต้องสร้างสมการที่มีตัวแปรที่ 3 ด้วย
วิเคราะห์ผลด้วย Hirarchical regression
อย่าลืมตรวจสอบข้อตกลงเบื้องต้นของข้อมูลก่อนนะค้า
ข้อตกลงเบื้องต้นของการใช้สมการถดถอยเส้นตรง (linear regression)
- Linear relationship : คือ x และ y มีแนวโน้มที่จะเป็นเส้นตรง
- Independence : คือการที่ residuals (ค่าหลงเหลือจากการขีดเส้นตรง) มีความแยกออกจากกัน
- Homoscedasticity : คือการที่ residuals มีความสม่ำเสมอในทุก ๆ ช่วงของ x
- Normality : คือการที่ residuals มีโค้งปกติ Note* อันนี้คือค่า residuals ไม่ใช่ค่าข้อมูลนะ
- Multi-collinearity: คือการที่ตัวแปร x มีความสัมพันธ์กันสูง จะทำให้ผลที่ได้มีความอคติ
ใน R นี้เราจะทดสอบข้อที่ 1, 3, 4, และ 5
#สร้างโมเดลขึ้นมาก่อน
h.model1 <- lm(saving ~ . , data = data) #สร้างโมเดลครบทุกตัวแปร
#ทดสอบ Homoscedasticity
plot(h.model1, 1)
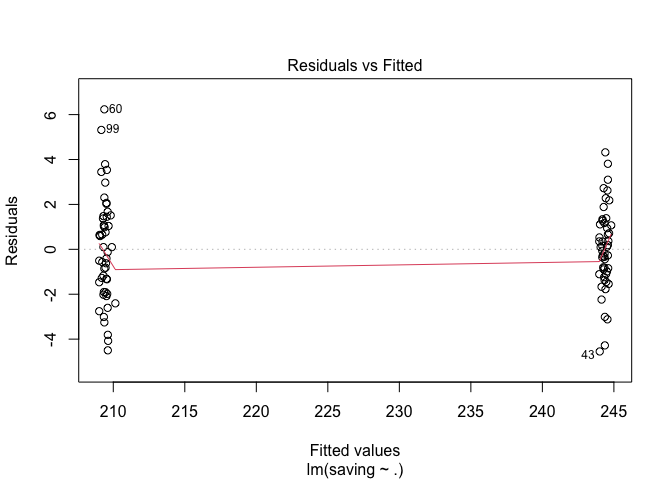
# ทดสอบ Normality
plot(h.model1, 2) #or
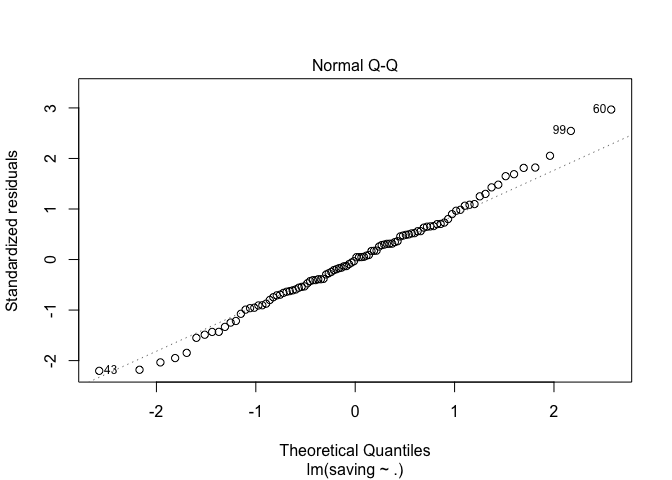
car::qqPlot(h.model1)
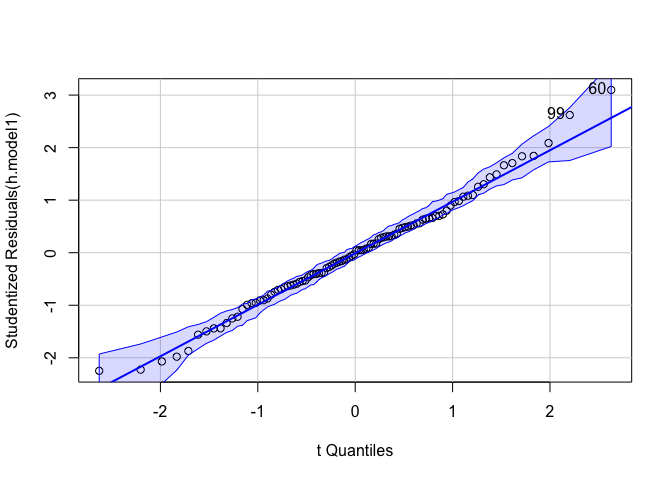
## [1] 60 99
# ทดสอบ linearity
plot(h.model1, 3) #or
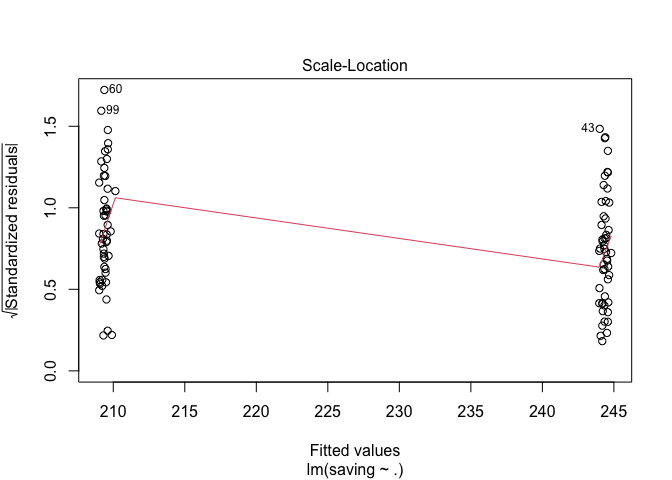
# ทดสอบ Multi-collinearity
car::vif(h.model1) # cutoff is 2.5
## gender age household
## 1.479374 1.467236 1.011553
ผลจากการทดสอบข้อตกลงเบื้องต้นไม่พบข้อมูลที่ละเมิดจนเกินไป เราสามารถใช้ boxplot() ในการดูข้อมูลเบื้องต้นได้อีกด้วย
boxplot(saving ~ gender, data = data)
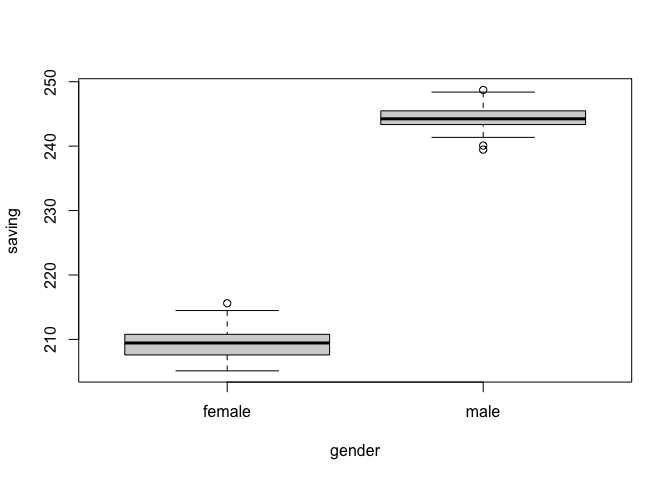
Note จะเห็นได้ว่าข้อมูลระหว่างกลุ่มของเราแยกออกจากกันชัดเจนมาก (นี่เป็นเพราะ SD ที่ใส่ตอนสร้าง data มีไม่กว้างพอและจำนวน N แคบ)
วิเคราะห์ผล
model.1 <- lm(saving ~ age + household, data)
summary(model.1)
##
## Call:
## lm(formula = saving ~ age + household, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.342 -10.915 -1.132 10.733 40.673
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 106.5609 17.7049 6.019 3.13e-08 ***
## age 3.9897 0.5971 6.682 1.49e-09 ***
## household 1.0769 1.0471 1.028 0.306
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.68 on 97 degrees of freedom
## Multiple R-squared: 0.3247, Adjusted R-squared: 0.3107
## F-statistic: 23.32 on 2 and 97 DF, p-value: 5.389e-09
จาก output จะเห็นได้ว่า เมื่ออายุเพิ่มขึ้น 1 ปี งินเก็บรายสัปดาห์ของคนจะเพิ่มขึ้น 3.7586 บาท อย่างมีนัยสำคัญทางสถิติ ในขณะที่เมื่อจำนวนคนในบ้านเพิ่มขึ้น จำนวนเงินเก็บจะลดลง -0.1825 บาท และตัวแปรต้นสามารถอธิบายโมเดลได้ 0.33 หรือ 33%
ใส่ตัวแปรที่ศึกษาเพิ่มในโมเดล คือ gender
model.2 <- lm(saving ~ age + household + gender, data)
summary(model.2)
##
## Call:
## lm(formula = saving ~ age + household + gender, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5497 -1.3182 0.0135 1.1974 6.2350
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 208.15206 2.97449 69.979 <2e-16 ***
## age 0.03198 0.10454 0.306 0.760
## household 0.14768 0.15222 0.970 0.334
## gendermale 34.81438 0.51715 67.319 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.126 on 96 degrees of freedom
## Multiple R-squared: 0.986, Adjusted R-squared: 0.9856
## F-statistic: 2252 on 3 and 96 DF, p-value: < 2.2e-16
จะพบว่าเมื่อใส่ตัวแปรเพศลงไปแล้ว อายุไม่มีนัยสำคัญในการทำนายจำนวนเงินเก็บต่อสัปดาห์อีกต่อไปแต่เมื่อเปรียบเทียบกับกลุ่มอ้างอิง (คือ ผู้หญิง) แล้ว ผู้ชายสามารถเก็บเงินได้มากกว่า 34.91 บาทอย่างมีนัยสำคัญทางสถิติ และตัวแปรต้นสามารถอธิบายโมเดลนี้ได้ 0.98 หรือ 98% (ในโลกความเป็นแบบนี้ไหมนะ >o<)
####ทดสอบความแตกต่างของโมเดล
anova(model.1, model.2)
## Analysis of Variance Table
##
## Model 1: saving ~ age + household
## Model 2: saving ~ age + household + gender
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 97 20916.2
## 2 96 433.9 1 20482 4531.9 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
จะพบว่าเมื่อเทียบกันทั้งสองโมเดลแล้ว มีความแตกต่างอย่างมีนัยสำคัญ p < 0.001 โดยที่ changed Rsquare อยู่ที่ 0.98 - 0.33 = 0.66 หรือ 66%
มาสร้างกราฟให้เป็นนิสัย
library(ggplot2)
##
## Attaching package: 'ggplot2'
## The following objects are masked from 'package:psych':
##
## %+%, alpha
ggplot(data) +
geom_bar(aes(x = gender, y = saving, fill = gender), stat = "summary") +
theme_classic() +
scale_fill_brewer(palette = 1)
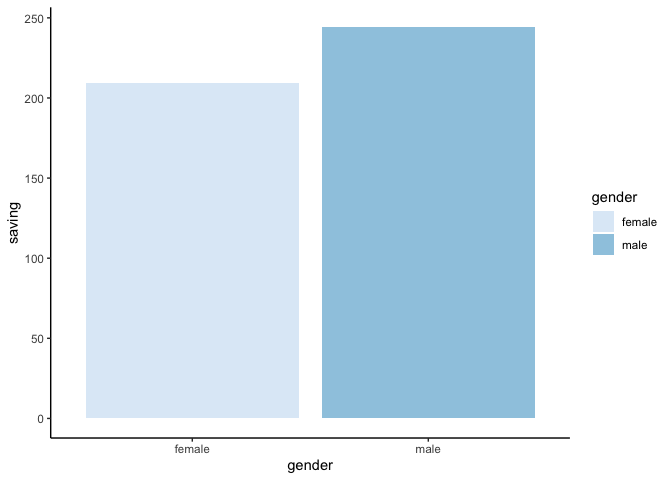
ทาด้า จบแล้วจ้า เดี๋ยวมีเสริมการใส่ตัวแปร dummy มากกว่า 2 ตัว ในสมการค่า~~
Happy Coding ka สามารถกดติดตามและ subscribe ได้ที่ datastist.com