One-sample t-test

การเปรียบเทียบค่าเฉลี่ยกลุ่มเมื่อรู้ค่าเฉลี่ยของกลุ่มประชากร

กลับมาที่ t-test ของเรา หลังจากที่ไปมึนอยู่กับ Central Limit Theorem

ในบทนี้ เราจะสร้างชุดข้อมูลง่าย ๆ ในการเปรียบกลุ่มประชากร ซึ่งหมายถึงการเปรียบเทียบค่าเฉลี่ยของกลุ่มตัวอย่าง (x-) กับค่าเฉลี่ยของประชากร ((μ)

สมมติว่า

แมวทั้งโลกมี 6,000,000 ตัว และนอนวันละ 21 ชั่วโมง เราไปเก็บข้อมูลชั่วโมงที่แมวนอนแถวซอยบ้านเรามา 30 ตัว

set.seed(1990)
cat_alley <- rnorm(n = 30, mean = 16.78, sd = 3.4)
cat_alley <- as.data.frame(cat_alley)
summary(cat_alley)

##    cat_alley    
##  Min.   :10.91  
##  1st Qu.:14.14  
##  Median :15.31  
##  Mean   :15.97  
##  3rd Qu.:17.54  
##  Max.   :22.77

เราลองมา plot graph เล่น ๆ ดู

library(ggplot2)
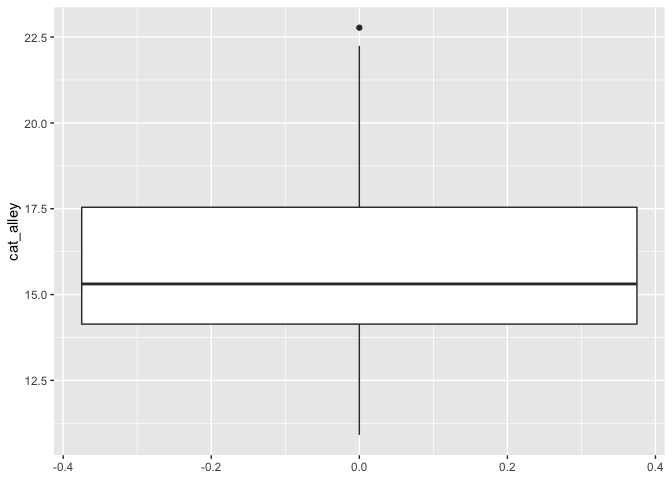
ggplot(cat_alley, aes(y = cat_alley)) +
      geom_boxplot()

ggplot(cat_alley, aes(x = cat_alley)) +
      geom_density()

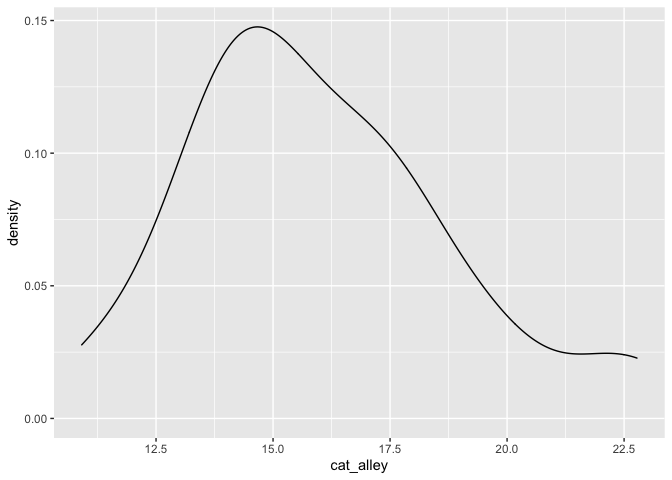
จะพบว่าข้อมูล cat_alley ที่เก็บมามีความเป็น Normal Distribution

จากโจทย์

แมวทั่วโลกมีค่าเฉลี่ยนอนวันละ 21 ชั่วโมง (μ)

ข้อตกลงเบื้องต้นของ One-sample t-test

การวิเคราะห์ผลโดยนำค่าเฉลี่ยจากกลุ่มตัวอย่าง (x-) ไปเปรียบเทียบกับค่าเฉลี่ยประชาชน ข้อมูลของกลุ่มตัวอย่างจำเป็นต้องผ่านข้อตกลงเบื้องต้น หรือ (assumption) ของการทดสอบสถิติดังกล่าว

ข้อตกลงเบื้องต้นของ One-sample t-test มีดังนี้

ตัวแปรตาม (dependent variable) หรือตัวแปร criterion ควรอยู่ในรูปของตัวแปรต่อเนื่อง (see: levels of measurements) ไม่ว่าจะเป็นแบบ interval หรือ ratio

จำนวนชั่วโมงที่แมวนอนเป็นแบบ ratio อยู่แล้ว
ข้อมูลมีความอิสระจากกัน (Independence; เราจะพบข้อตกลงนี้ในหลาย ๆ การทดสอบทางสถิติเพราะเป็นเรื่องที่สำคัญ, ดูเพิ่มเติมจาก concept) กล่าวคือ การออกแบบการเก็บข้อมูลจะต้องทำให้ไม่มีความสัมพันธ์ในกลุ่ม

สมมติว่าเก็บข้อมูลแบบสุ่มสมบูรณ์ (complete randomization)
ข้อมูลไม่ควรมีค่าสุดโต่ง (outliers) เพราะการใช้ค่าเฉลี่ย (mean) ในการคำนวณมีความเสี่ยงจะเกิดอคติสูง (see concept ทำไมถึงใช้ค่าเฉลี่ย)

จากกราฟ boxplot() ดูเหมือนจะไม่มีค่าสุดโต่ง (ทดสอบได้โดยใช้ +-3SD)
ตัวแปรตาม (dependent variable) ควรอย่างน้อยมีโค้งเป็นปกติ แม้ว่าการทดสอบ t จะค่อนข้างแข็งแกร่ง (robust) ต่อการเบ้ของข้อมูลก็ตาม เราสามารถทดสอบได้ด้วย Shapiro-Wilk test of normality

ดูจาก plot(density()) ก็มีความโค้งปกติอยู่ อาจจะใช้ car::qqPlot(data) ร่วมด้วยก็ได้

การวิเคราะห์ผลสถิติ t แบบ one-sample

สมมติฐานว่างของเราในที่นี้คือ

Ho : μ = 21 
or
Ho : μ - 21 = 0

เมื่อทดสอบด้วยสถิติ t จะพบว่า

t.test(cat_alley, mu = 21)

## 
##  One Sample t-test
## 
## data:  cat_alley
## t = -9.7915, df = 29, p-value = 1.062e-10
## alternative hypothesis: true mean is not equal to 21
## 95 percent confidence interval:
##  14.92281 17.02292
## sample estimates:
## mean of x 
##  15.97286

ผลจากการวิเคราะห์ t.test() พบว่า แมวในซอยบ้านเรามีชั่วโมงนอนเฉลี่ยแตกต่างจากแมวทั่วโลกอย่างมีนัยสำคัญทางสถิติที่ค่า t(1, 29) = -9.79, p < 0.001 ค่ะ

Happy Coding ka สามารถกดติดตามและ subscribe ได้ที่ datastist.com