Correlation
ทำความคุ้นเคยกับความสัมพันธ์แบบเส้นตรง
ความสัมพันธ์ สหสัมพันธ์ หรือ Pearson’s product correlation (r)
การทดสอบ correlation คือการทดสอบความสัมพันธ์ระหว่างตัวแปร 2 ตัว ซึ่งจะทำให้เรารู้ว่า เมื่อตัวหนึ่งเพิ่มขึ้นอีกตัวเพิ่มขึ้นตามไหม
ตัวอย่าง

การบริโภคกาแฟเฉลี่ย และน้ำหนักเฉลี่ย มีความสัมพันธ์กับนักเรียนแต่ละชั้น (grade 1 - 12)
ในบทนี้ เราจะสร้าง dataframe ขึ้นมาด้วย r
Grade <- 1:12
Avg_weight <- c(48, 54, 61, 69, 74, 85, 89, 99, 110, 100, 114, 150)
Avg_coffee <- c(6, 7, 1, 0, 4, 6, 4, 4, 7, 7, 7, 7)
data <- cbind(Grade, Avg_weight, Avg_coffee)
head(data)
## Grade Avg_weight Avg_coffee
## [1,] 1 48 6
## [2,] 2 54 7
## [3,] 3 61 1
## [4,] 4 69 0
## [5,] 5 74 4
## [6,] 6 85 6
หลังจากนั้นเราจะใช้ scatter plot ด้วยคำสั่ง scatter.smooth() ในการดูความสัมพันธ์ด้วยสายตาของ Grade กับ น้ำหนักเฉลี่ย (Avg_weight)
scatter.smooth(Grade, Avg_weight, family = "gaussian")
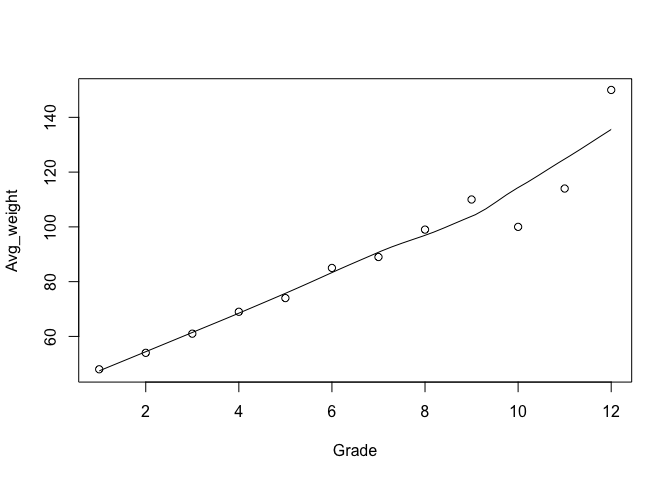
กราฟแสดงถึงการที่ยิ่ง Grade สูงขึ้นเท่าไหร่ น้ำหนักก็จะสูงขึ้น ซึ่งสมเหตุสมผล (โตขึ้น น้ำหนักมากขึ้น)
ที่นี้เรามาดูความสัมพันธ์ของ Grade กับ ค่าเฉลี่ยจำนวนกาแฟที่ดื่มต่อสัปดาห์
scatter.smooth(Grade, Avg_coffee, family = "gaussian")
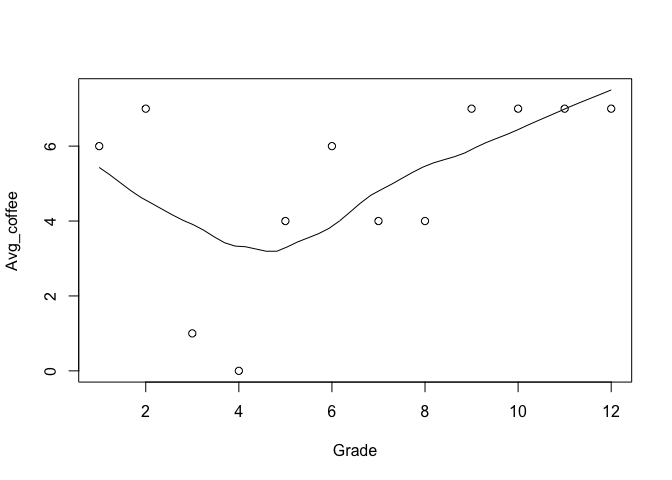
จะเห็นได้ว่า Grade และ จำนวนกาแฟเฉลี่ยที่กิน ไม่มีความสัมพันธ์กัน
ถ้าความสัมพันธ์ของทั้งสองตัวแปรเป็นเส้นตรงและมีความชันสูงก็ยิ่งมีความสัมพันธ์กันสูง
-
ความสัมพันธ์ที่เท่ากับ 0 หมายถึงไม่มีความสัมพันธ์ใด ๆ ของตัวแปร
-
ความสัมพันธ์ระหว่าง -1 หรือ 1 แสดงถึงการมีความสัมพันธ์ ยิ่งค่ามีความใกล้ -1 (เช่น -0.98) หรือ 1 (เช่น 0.8) แสดงถึงความความสัมพันธ์ที่มีมาก ในขณะที่ความสัมพันธ์ประมาณ -0.5 หรือ +0.5 แสดงถึงความสัมพันธ์เบา ๆ
เรามาลองทดสอบความสัมพันธ์ของตัวแปรกัน ด้วยำสั่ง cor.test()
cor.test(Grade, Avg_weight)
## Pearson's product-moment correlation
##
## data: Grade and Avg_weight
## t = 10.996, df = 10, p-value = 6.614e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8632963 0.9893030
## sample estimates:
## cor
## 0.9610489
จะเห็นได้ว่า จากผลการทดสอบของ Pearson’s correaltion ของ Grade และ Avg_weight มีความสัมพันธ์กันที่ 0.961 อย่างมีนัยสำคัญทางสถิติที่ p < 0.001
ที่นี้มาดูความสัมพันธ์ของ Grade และ Avg_Coffee กันบ้าง
cor.test(Grade, Avg_coffee)
## Pearson's product-moment correlation
##
## data: Grade and Avg_coffee
## t = 1.5609, df = 10, p-value = 0.1496
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.1759887 0.8106090
## sample estimates:
## cor
## 0.4426174
จากผลการทดสอบของ Pearson’s correaltion Grade และ Avg_Coffee มีความสัมพันธ์กันที่ 0.442 ซึ่งไม่ถึงนัยสำคัญทางสถิติ
Happy Coding ka สามารถกดติดตามและ subscribe ได้ที่ datastist.com