Normal distribution in Real Dataset
จากบทที่แล้ว เราเริ่มรู้ว่าทำไมนักวิจัยหรือนักสถิติ (ที่ใช้สถิติบางประเภท) มีข้อตกลงเบื้องต้นว่าข้อมูลควรจะมีแนวโน้มเข้าสู่ศูนย์กลาง (normally distributed) บทนี้เราจะมาลอง dataset จริงจากการสร้างชุด data ขึ้นมา โดยการสุ่มเลขและใช้ package ชื่อว่า random
install.packages("random")
library("random")
random <- as.data.frame(randomNumbers(n = 2100, min = 0, max = 40, col = 3))
head(random)
## V1 V2 V3
## 1 4 1 33
## 2 30 27 34
## 3 33 26 14
## 4 33 12 13
## 5 17 24 22
## 6 38 0 1
summary(random)
## V1 V2 V3
## Min. : 0.00 Min. : 0.00 Min. : 0.00
## 1st Qu.:10.00 1st Qu.:10.00 1st Qu.:10.00
## Median :21.00 Median :20.00 Median :20.00
## Mean :20.44 Mean :19.92 Mean :20.07
## 3rd Qu.:31.00 3rd Qu.:30.00 3rd Qu.:30.00
## Max. :40.00 Max. :40.00 Max. :40.00
เราจะได้ dataset 1 ชุดที่มี 3 คอลลัมภ์ (V1, V2, V3) ถ้าเราลองนำข้อมูลในแต่ละคอลลัมภ์มา plot density graph
den_V1 <- plot(density(random$V1))
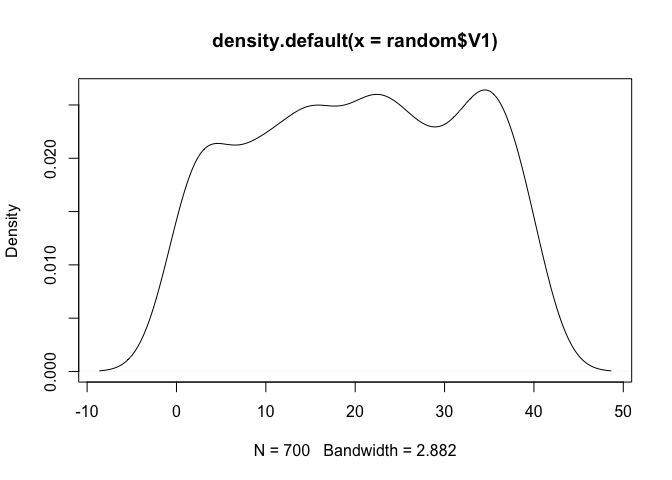
den_V2 <- plot(density(random$V2))
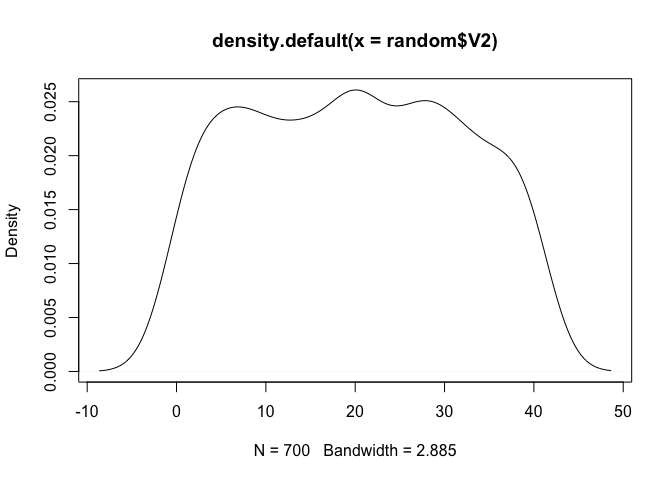
den_V3 <- plot(density(random$V3))
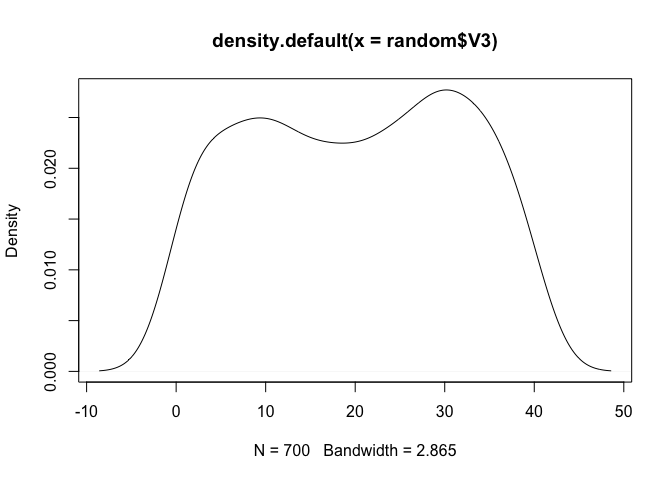
ถามว่าโค้งปกติไหม ตอนนี้อาจจะดูงง ๆ สุด ๆ แต่เราสามารถทดสอบได้ด้วยคำสั่ง qqPlot() จาก package car *P ตัวใหญ่
library(car)
qqPlot(random$V1)
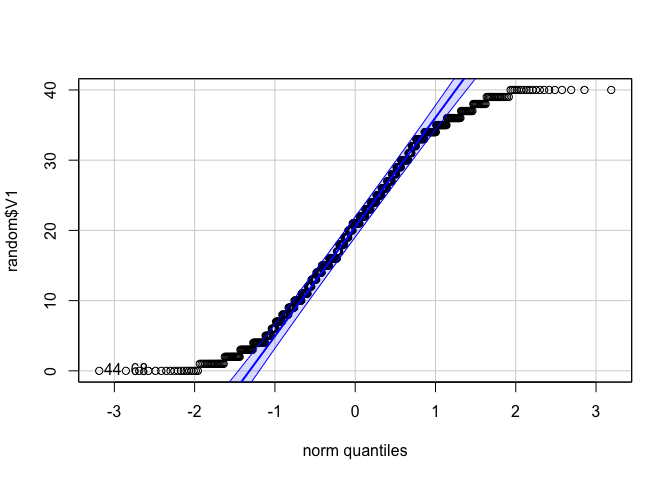
## [1] 44 68
qqPlot(random$V2)
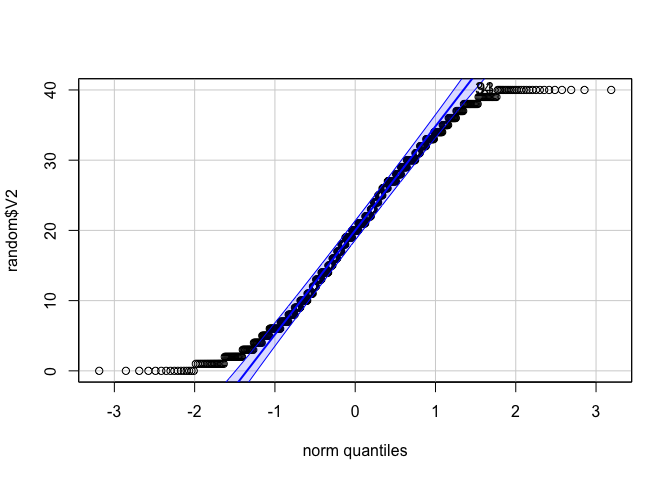
## [1] 34 93
qqPlot(random$V3)
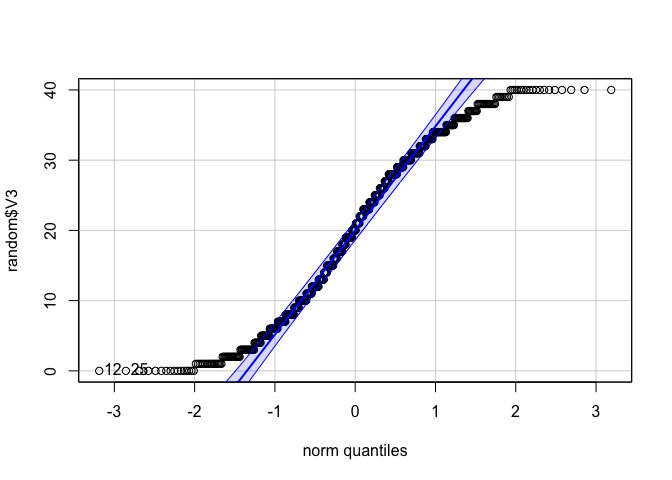
## [1] 12 25
จะเห็นได้ว่า ข้อมูลเรียบเคียงไปตามเส้นที่ควรจะเป็น
แต่ถ้าเราอยากเห็นว่าถ้ามี data ที่สุดโต่งขึ้นมา (outliers) จะเป็นอย่างไร เราจะลองใส่ข้อมูลใน data ที่เรามีอยู่
random[c(1, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100), "V1"] <- 69
qqPlot(random$V1)
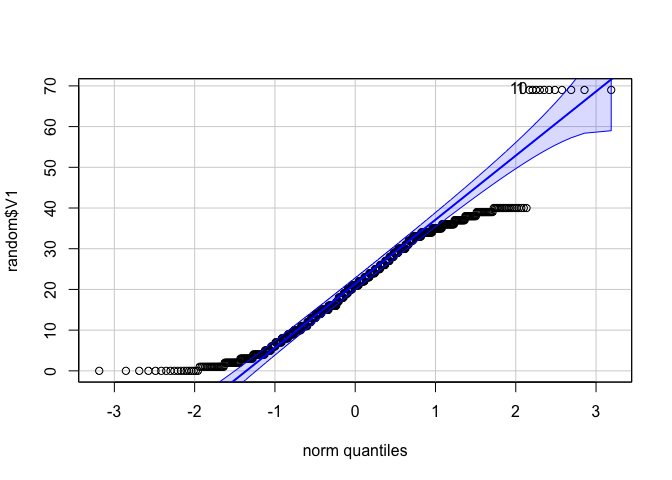
## [1] 1 10
ที่นี้เราจะเห็นชัดมากขึ้นว่า Q-Q plotเราเริ่มงงตัวมันเองแล้ว
ถ้าจะให้ชัดเจนเมื่อข้อมูลมีOutliers หรือ ค่าสุดโต่ง เราสามารถที่จะสร้างกราฟด้วยคำสั่ง boxplot() ได้
boxplot(random$V1)$out
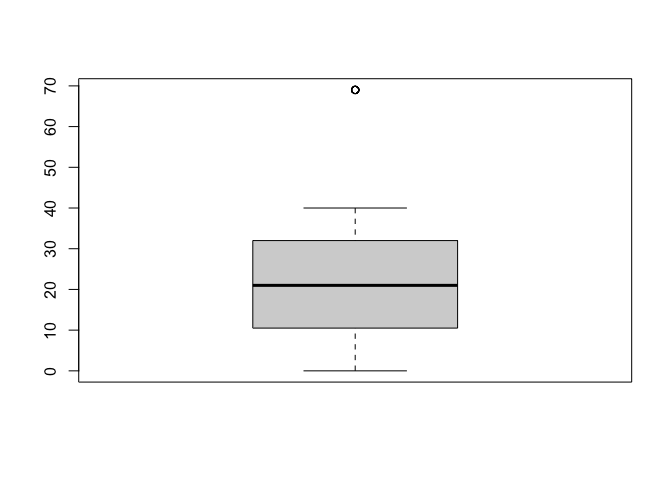
## [1] 69 69 69 69 69 69 69 69 69 69 69
พอเป็น boxplot()เราก็จะเห็นชัดเจนขึ้นมากว่าค่าสุดโต่งคือเลข 69
การแทนที่ค่าสุดโต่งหรือกำจัดออกไปขึ้นอยู่กับสายงานวิจัยของเรา การวิจัยทางจิตวิทยาอาจให้ตัดค่าที่มีค่าสูงกว่า +3SD หรือ -3SD เราจะไปพูดถึงอีกทีในการทำความสะอาดข้อมูล (data cleaning)ค่า~