Hypothesis Testing
การทดสอบสมมติฐาน
จำงานวิจัยที่ผู้ชายและผู้หญิงกินโดนัทได้ไหม?
สมมติว่า

ผู้ชายกินโดนัทเฉลี่ย 6 ครั้งต่อสัปดาห์ ในกลุ่มตัวอย่างชาย 40 คน ในขณะที่ผู้หญิงกินโดนัทเฉลี่ย 8 ครั้งต่อสัปดาห์ ในกลุ่มตัวอย่างผู้หญิง 70 คน
มองคร่าวๆ เราอาจสรุปไม่ได้ว่าค่าเฉลี่ย 6 ครั้งของผู้ชาย และ 7 ครั้งของผู้หญิงต่างไหม แล้วมีวิธีใดบ้างที่ทำให้เรารู้ว่ามันต่างกันไหม
a : ต่างสิ แค่เห็น 6 กับ 7 ก็ต่างกันละ
b : แต่แกต้องดูว่าเก็บมาจากกลุ่มตัวอย่างกี่คนด้วย ชาย 40 หญิง 70 เอามาเทียบกันได้ไง
c : แล้วความแตกต่างของแต่ละคนจะเอาค่าเฉลี่ยเทียบเลยไม่ได้นะ
Hypothesis Testing
จากบทก่อนหน้านี้ เราอาจจะเริ่มเรียนรู้ว่าข้อมูลในโลกความจริงโดยเฉพาะที่มาจากกลุ่มตัวอย่างมีความกำกวมสูง นักสถิติจึงคิดค้นวิธีการคำนวณการเปรียบเทียบหรือความสัมพันธ์ของข้อมูลที่เก็บมา
คำถามคือ “ทำอย่างไรให้ข้อมูลที่เก็บมาสะท้อนถึงข้อมูลของประชากรจริงๆ มากที่สุด?”
ในทางวิจัย อาจมีวิธีการเก็บข้อมูลที่จะช่วยให้ได้กลุ่มตัวอย่างที่สะท้อนถึงประชากรในขณะเดียวกัน เชิงสถิติ ข้อมูลที่เก็บมาจากกลุ่มตัวอย่างจะถูกเรียกว่าโค้งกลุ่มตัวอย่าง หรือ sampling distribution
เราจะเรียนรู้จักการสร้าง data ขึ้นมาจากโจทย์โดนัท
set.seed(1990) #เซ็ทไว้สำหรับการทำซ้ำ
male_donut <- rnorm(40, mean = 6, sd = 1)
hist(male_donut)
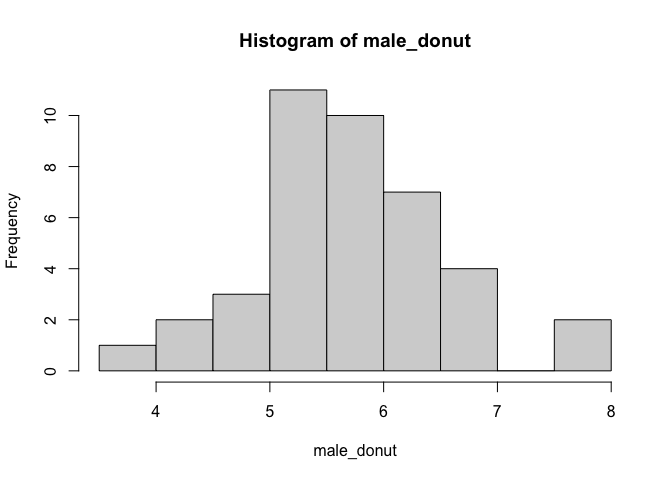
female_donut <- rnorm(70, mean = 8, sd = 1)
hist(female_donut)
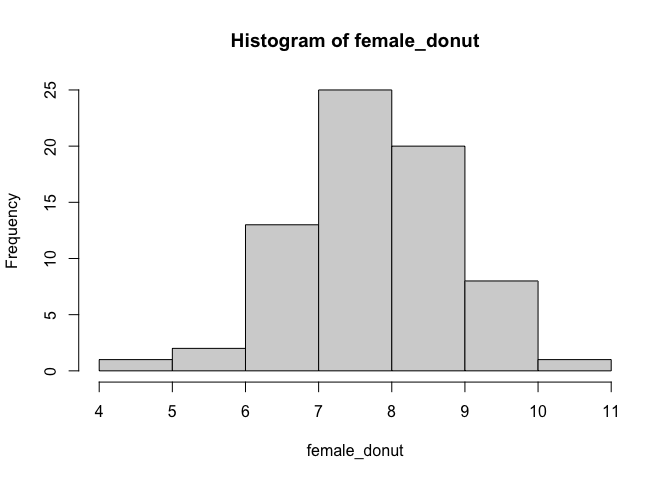
Gender <- c(rep("male", 40), c(rep("female", 70))) #แปลงไฟล์ ใส่เพศลงไป
male_donut <- as.data.frame(male_donut)
female_donut <- as.data.frame(female_donut)
colnames(female_donut) <- "donut" #ให้คอลลัมภ์จำนวนชิ้นชื่อว่า "donut"
colnames(male_donut) <- "donut" #ให้คอลลัมภ์จำนวนชิ้นชื่อว่า "donut"
donut <- rbind(male_donut, female_donut) #rbind() ใช้รวบข้อมูลแถวเข้าด้วยกัน
data_donut <- cbind(Gender, donut) #cbind ใช้รวบคอลลัมภ์เข้าด้วยกัน
ในตัวอย่างนี้จะใช้ package ggplot2 ในการสร้างกราฟ
library(ggplot2)
ggplot(data_donut) + geom_density(aes(x=donut, fill=Gender), alpha=.5)
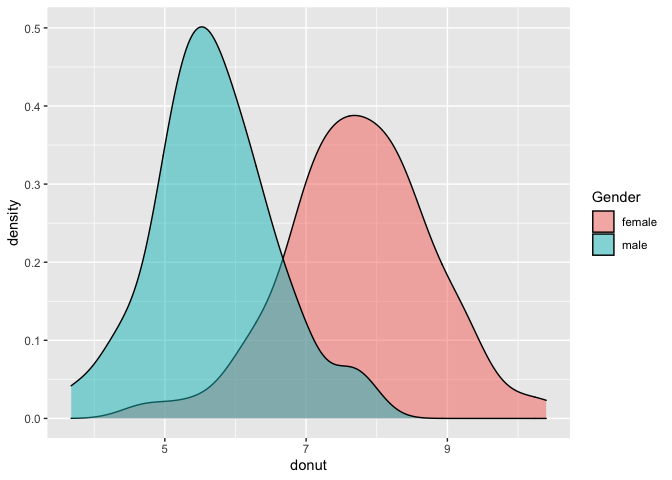
เมื่อนำกราฟมาเปรียบเทียบกันระหว่างชายและหญิงจะพบว่ามีพื้นที่ที่ซ้อนทับกันอยู่
ถ้าเราทำการวิจัยอยู่บนข้อมูลนี้ เราจะต้องตั้งคำถามการวิจัยขึ้นมาก่อน
a : ผู้หญิงกินโดนัทมากกว่าผู้ชายชัวร์
b : ฉันเห็นผู้ชายชอบกินของหวานออก
c : เราว่ามันน่าจะพอ ๆ กันแหละ
แล้วเราควรจะตั้งคำถามงานวิจัยว่าอย่างไร?
การตั้งคำถามงานวิจัย
Research hypothesis หรือ คำถามในการวิจัย จะเป็นธงให้เราทดสอบและตั้งคำถามสถิติ รวมไปถึงการสรุปงานวิจัยในภายภาคหน้านู่นด้วย ในกรณีการกินโดนัท สมมติว่า คำถามของงานวิจัยเราคือ
ผู้หญิงกินโดนัทเฉลี่ยต่อสัปดาห์มากกว่าผู้ชาย
เราจะได้คำถามเชิงสถิติขึ้นมา เรียกว่า สมมติฐานว่าง หรือ (null hypothesis; H0) สมมติฐานนี้จะสันนิษฐานว่ากลุ่มตัวอย่างมีค่าเฉลี่ยเท่ากัน คือ
x̄ การกินโดนัทต่อสัปดาห์ของผู้ชาย != x̄ การกินโดนัทต่อสัปดาห์ของผู้หญิง
Note เครื่องหมายไม่เท่ากับใน R คือ !=
ในขณะที่สมมติฐานทางเลือก (alternative hypothesis; Ha) จะสันนิษฐานว่ามีค่าเฉลี่ยกลุ่มใดกลุ่มหนึ่งมีค่ามากกว่า/น้อยกว่ากันอย่างมีนัยสำคัญทางสถิติ
นัยสำคัญทางสถิติ (BRB)
ในส่วนของการทดสอบสมมติฐาน เราจะทดสอบสมมติฐานว่าง (Ho) โดยคิดว่ามันเป็นจริง จากนั้นเราจะไปเก็บข้อมูล และ มีข้อสรุปว่าเราจะ “ปฎิเสธสมมติฐานว่างว่าเป็นจริง” หรือ “คงไว้ซึ่งสมมติฐานว่าง” (Howell, 2017)
ว่าแต่ สรุปใครกินโดนัทมากกว่ากัน? >o<
การทดสอบสมมติฐาน Ho
ก่อนหน้านี้เราเคยเอ่ยถึง sample statistics ที่มีความหมายถึงค่าใด ๆ ที่มาจากกลุ่มตัวอย่าง (sample) การทดสอบทางสถิติมีความแตกต่างออกจากค่าเหล่านั้น เราจะเรียกการทดสอบนี้ว่า test statistics
Test statistics
การทดสอบความแตกต่าง อิทธิพล หรือความน่าจะเป็น จะต้องอาศัย test statistics เข้ามาช่วยในการวิเคราะห์ ซึ่งเราอาจจะเคยเห็นผ่านตาในรูปแบบของ t-Test, F-Test, หรือ χ2-Test(และอื่น ๆ อีกมากมายนัก)
การทดสอบว่าผู้ชายกินโดนัทแตกต่างจากผู้หญิงหรือไม่ เป็นการทดสอบระหว่างกลุ่ม (factor) และ ค่าจำนวนชิ้นโดนัท (numeric; กลับไปดู scale of measurement) ดังนั้น การทดสอบดังกล่าวจึงใช้ t-Test ทั้งนี้ เราจะยังไม่ลงรายละเอียดใด ๆ
t.test(donut ~ Gender, data = data_donut, var.equal = TRUE)
## Two Sample t-test
##
## data: donut by Gender
## t = 10.703, df = 108, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## 1.672317 2.432523
## sample estimates:
## mean in group female mean in group male
## 7.748332 5.695912
ผล output ของ R แสดงถึงความแตกต่างระหว่างกลุ่มเพศหญิง (M = 7.75) และเพศชาย (M = 5.70) ในจำนวนชิ้นของโดนัทที่กินในแต่ละสัปดาห์อย่างมีนัยสำคัญทางสถิติ (t(1,108) = 10.703, p < 0.001) จึงปฎิเสธสมมติฐานว่างที่ว่าค่าเฉลี่ยของทั้งสองกลุ่มจะเท่ากัน
นักวิจัยจะพยายามเขียนผลการวิเคราะห์ที่ออกมาประมาณนี้ ถ้าเราแปลตามภาษาดาวแมวแล้ว เราสามารถสรุปได้ว่า
- เพศหญิงกินโดนัทมากกว่าเพศชายแน่ ๆ
- เพศหญิงและเพศชายกินโดนัทจำนวนแตกต่างกัน
- เพศหญิงและเพศชายมีโอกาสกินโดนัทเท่ากันน้อยกว่า 1 ใน 1000
แต่!! แมวทั้งหลาย อย่าลืมว่านี่เป็น dataset ที่มโนขึ้นมาล้วน ๆ จ้า >w<
บทต่อไปเราจะพูดถึงการปฎิเสธสมมติฐานว่าง (null hypothesis; Ho) หรือยอมรับสมมติฐานทางเลือก (alternative hypothesis; Ha)
Happy Coding ka สามารถกดติดตามและ subscribe ได้ที่ datastist.com