Confident Interval

เวลาที่เราได้ผลวิเคราะห์จากโปรแกรมใด ๆ ก็ตามออกมา ลูกแมวอาจจะคิดว่า

“นี่ไง p-value ก็บอกเราได้แล้วว่า significant หรือเปล่า”

ถูกค่ะ

แต่เรามารู้จัก parameter อีกตัวที่จะคอย support ผลวิเคราะห์ของเรา นั่นก็คือ CI : Confident Interval

Confident Interval ในเชิงทฤษฎี

ช่วงความเชื่อมั่น หรือ Confident Interval เป็นค่าที่บอกความไม่มั่นใจของการสุ่มข้อมูลจากกลุ่มตัวอย่าง โดยปกติแล้วเราจะให้ช่วงความเชื่อมั่นนี้อยู่ที่ 0.95 หรือ 0.99 และสร้างอยู่รอบ parameter ที่เราใช้ทดสอบ (เช่น ค่าเฉลี่ย)

ในเชิงทฤษฎีแล้ว CI อาจสามารถเขียนสมการได้ ดังนี้

.95 CI = X¯ ± (critical point of statistical test) * se

Confident Interval ในเชิงโลกแมว

ค่า CI ในโลกของแมว ก็คือช่วงความเชื่อมั่นที่เราจะพบว่าผลที่เราต้องการตกอยู่ในช่วงนี้เท่าไหร่

หายใจลึก ๆ

ยกตัวอย่าง เช่น

donut

ผู้ชายกินโดนัทเฉลี่ย 6 ครั้งต่อสัปดาห์ ในกลุ่มตัวอย่างชาย 40 คน ในขณะที่ผู้หญิงกินโดนัทเฉลี่ย 8 ครั้งต่อสัปดาห์ ในกลุ่มตัวอย่างผู้หญิง 70 คน

set.seed(1990)
male_donut <- rnorm(40, mean = 6, sd = 1)
female_donut <- rnorm(70, mean = 8, sd = 1)
Gender <- c(rep("male", 40), c(rep("female", 70)))
male_donut <- as.data.frame(male_donut)
female_donut <- as.data.frame(female_donut)
colnames(female_donut) <- "donut"
colnames(male_donut) <- "donut"
donut <- rbind(male_donut, female_donut)
data_donut <- cbind(Gender, donut)

# t.test
t.test(donut ~ Gender, data = data_donut, var.equal = TRUE, conf.level = 0.95)

## 
##  Two Sample t-test
## 
## data:  donut by Gender
## t = 10.703, df = 108, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
##  1.672317 2.432523
## sample estimates:
## mean in group female   mean in group male 
##             7.748332             5.695912

จาก output t.test() เรื่องจำนวนโดนัท เราจะเห็นบรรทัดนี้

95 percent confidence interval:
 1.672317 2.432523

เมื่อคิดดี ๆ Ho ของเราใน t-Test นี้คือ

meanMale = meanFemale 
ก็แปลว่า
Xmale - Xfemale = 0

ดังนั้น ถ้าค่า CI อยู่ระหว่าง 1.672317 ถึง 2.432523 ไม่คร่อมเลข 0ก็แปลว่ามีนัยสำคัญนี่เอง!!!!

a : อ้าว แล้วมันต่างอะไรกับ p-value ละคะ

ต่างสิ แต่ก็มาจาก parameter ในสมการคล้าย ๆ กัน เพราะ CI บอกช่วงความกว้าง

ยิ่งใกล้ 0 มากเท่าไหร่แปลว่าอาจมี Type I error เกิดขี้น
ยิ่งกว้างเท่าไหร่แปลว่าข้อมูลของเรามีความเบี่ยงเบนจากค่า mean ไปเยอะ อาจเกิดเป็น error ในการสุ่มได้

นี่แหละแมว ความสำคัญของ confident interval

เราลองมาหาขนาดอิทธิพลดูดีกว่า

Ttest <- t.test(donut ~ Gender, data = data_donut, var.equal = TRUE, conf.level = 0.95)
effectsize::cohens_d(Ttest, pooled_sd = FALSE)

## Cohen's d |       95% CI
## ------------------------
## 5.06      | [4.38, 5.78]

plot graph ให้เป็นกิจวัตร

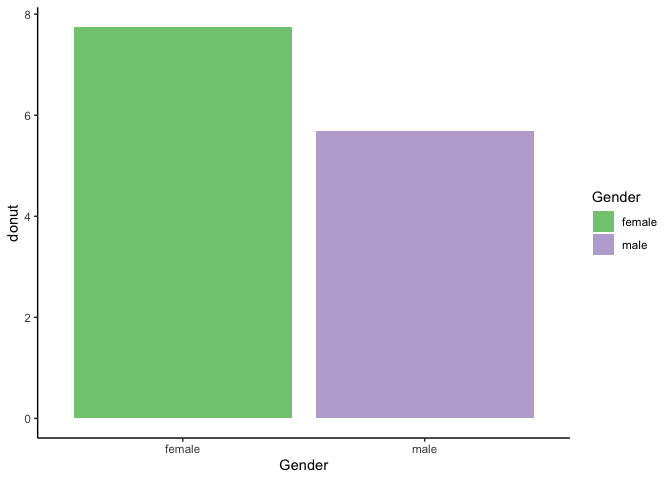
Bar Chart ให้ข้อมูลที่มีลักษณะเป็นกลุ่ม

library(ggplot2)
ggplot(data_donut, aes(x = Gender, y = donut, fill = Gender)) +
  geom_bar(stat = "summary") +
  theme_classic() +
  scale_fill_brewer(palette="Accent")

Density Chart ให้ข้อมูลความหนาแน่นของโค้ง

library(ggplot2)
ggplot(data_donut, aes(x = donut)) +
  geom_density(aes(fill = Gender), alpha = 0.5) +
  geom_vline(xintercept = c(4.38,5.78), color = "gray", linetype = "dashed") + 
  theme_classic() +
  scale_fill_brewer(palette="Accent")

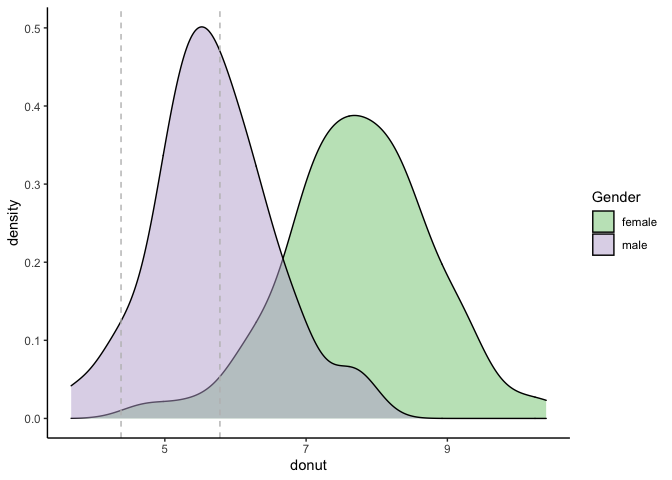
จะเห็นได้ว่าเส้นสีเท่าคือช่วงของ effect size cohens’ d ซึ่งจะบอกความแรง ความแตกต่างของข้อมูลทั้งสองกลุ่ม เดี๋ยวเราจะกลับมาเรียนเรื่อง effect size อีกที รอหน่อยน้า ~

Happy Coding ka สามารถกดติดตามและ subscribe ได้ที่ datastist.com